El último teorema de Fermat y la unidad de la ciencia
El último teorema de Fermat era hasta hace unos quince años uno de lo grandes problemas irresueltos de la matemática. Fue planteado por Pierre de Fermat hace alrededor de 300 años y plantea que la siguiente ecuación:
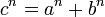 donde n>2.
donde n>2.
no tiene solución en números enteros.
Obviamente, esta no es más que una generalización del famoso teorema de Pitágoras. Lo interesante es que Fermat no era un matemático académico sino más bien lúdico y no se preocupaba demasiado en obtener demostraciones codificadas, replicables (y con todos los atributos que uno podría esperar en una demostración científica) sino que cuando había consideraba que había demostrado una conjetura, pasaba a la siguiente.
Esto es lo que pasó con el último teorema. Lo dejó anotado en el margen de un libro, la Arithmetica de Diofanto:
Es imposible dividir un cubo en suma de dos cubos, o un bicuadrado en suma de dos bicuadrados, o en general, cualquier potencia superior a dos en dos potencias del mismo grado; he descubierto una demostración maravillosa de esta afirmación. Pero este margen es demasiado angosto para contenerla.
Entonces, a partir de la suposición de que la demostración era posible (en tanto Fermat planteó que tenía una) hubo 3 siglos de matemáticos que intentaron replicarla. Solamente en 1996 un matemático llamado Andrew Wiles lo logró, pero utilizando técnicas sumamente avanzadas y que, de seguro, estaban fuera del alcance de Fermat en sus tiempos.
Ahora bien, más allá de la cuestión anecdótica de la historia del teorema lo que me resulta interesante y provocativo es pensar algunas de las siguientes afirmaciones:
a) en una ciencia que es algo así como el paradigma de la racionalidad y el método científico (al menos para muchos) una simple anotación marginal, una anotación que en términos reales era una afirmación arbitraria e indemostrada (tal y como plantea Singh en el libro, en realidad debería haber sido llamada la “conjetura de Fermat” y no el teorema)… digo, como en esta ciencia una afirmación tal, marcó el programa de investigación durante casi 200 años. Es llamativo, ¿no?
b) como a partir de ese problema, se fueron generando nuevos descubrimientos, nuevas técnicas en la ciencia matemática. Tal y como plantea Singh parece raro plantear la noción de “descubrimiento” en una ciencia formal como la matemática, pero de última, cuando (y otros) en el libro se ve como aparecen algunas nociones básicas, como las de números complejos, imaginarios, etc. e incluso el mismo teorema de Fermat y su resolución, parece difícil no utilizar ese concepto.
c) pensar en el problema de la “interdisciplinariedad” no es tan exclusivo de las ciencias experimentales, ni de las ciencias sociales. La demostración de Wiles constituyó algo así como la unificación de campos de la matemática (disciplinas) que estaban asiladas entre sí: la topología y la teoría de números
En fin, como para volver a acordarse de aquello de “unidad de la ciencia”. Si uno se saca la anteojera postmoderna vería que la ciencia es mucho más unitaria de lo que se puede pensar. Y que la separación “epistemológica” “ciencia dura”/ “ciencia blanda” o similares (“social”/ “natural”) parecen más bien una caricaturización de la realidad práctica.

Comentarios
Vaya usted, por qué carriles se anda metiendo... de Kondratieff a Wiles!
Ahora puede seguir con 'el teorema del loro' de Denis Guedj
[lo de la 'unidad' que mencionase puede experimentar en pequeña escala cuando se aprende algebra lineal, y se descubre iluminada por la misma luz una variedad de temas y problemas en apariencia inconexos: ecuaciones diferenciales, resolución de sistemas lineales, aproximaciones cuadráticas, etceterísima]
Si, el libro es bueno, pedagógico y todo. Pero hay una cosa que me molestó: la idealización de la matemática. Ya escribiremos algo sobre el tema...
Vi un programa de tv sobre esto y no es tan sencillo inclusive la solución.
Segundo que el problema se resuelva a partir de análisis numérico y no funcional, como tradicionalmente la matemática plantea sus cuestiones, esto hace que es la computadora, en realidad la que aproxima una solución que el científico después se las rebusca para formular matemáticamente.
Esto nos lleva al campo de la complejidad, por un lado la matemática de los números complejos rompe con todas las cabezas, de hecho la teoría de la relatividad es dificil de entender debido justamente a eso.
Complejidad y no linealidad van de la mano, por eso las metáforas y las abstracciones mentales que uno pueda realizar son inteligibles.
Esto nos lleva al concepto de No linealidad que desde el método plantea Edgar morín que hoy se ha convertido en un gurú de tipo místico.
En este mundo hay mucho chanta que dice esto es muy complejo o es una reducción de la complejidad, etc, etc, o como hace fermat, plantea la pregunta y se va a dormir la siesta.
Creo que vos, incluso, planteaste algo similar.
Final del cuento: Bateson, von Bertalanffy, Maturana no se plantean ante los problemas del lados de la soluciones, sino desde el lado del problema.
En realidad lo que importa a este científico es plantear una buena pregunta, descularla y dejar planteada otra, no la solución individualista tipo Sherlock.
esta solución plantea este tipo de problemas.
O sea partiendo de una motivación individualista, egosita, materialista, la guita; se llega a un tipo de solución que es abridora de caminos mas que encontradora de soluciones.
En esto, y a dichos de Maturana, el científico deberá ser impecable en el planteo del problema, y ese será su única contribución a la ciencia, no en el planteo de la solución magistral, el Daniel descifrador de signos de la biblia que Viñas toma como paradigma de este personaje.
Tampoco se puede decir que Andrew Wiles lo resolvió, por lo menos no como Pitágoras, arrimó el bochazo y deja planteada la cosa como para seguir investigando.
De hecho el tipo llega a la creencia que él estaba en buen camino mucho antes de que se publiquen los resultados, entonces rompe con el mundo y con su failia y se encierra en un altillo de su casa a presentar la pregunta, o la respuesta, como quiera llamarlo. Presentar el rpoblema de una forma impecable y entendible mas o menos. Como cuando copérnico escribe De revolutiónibus Orbium celestium durante cuarenta años y donde la teoría copernicana ocupa creo que un solo volumen de los ocho de su obra. El resto era gilada para que la iglesia, y su propia convicción religiosa, no se lo chupen.
Es válida la intuición, es casi el único sentido, es vaálida la pregunta , no la respuesta, en eso el científico postmoderno debe ser impecable.
Estoy de acuerdo en que Bateson y Bertalanffy plantearon las cosas del lado de los problemas más que de las soluciones - y ese es el punto: la definición de un campo de investigación tiene que ver con los problemas que uno se plantee. La pauta que conecta es un problema y un proyecto, antes que una meta. Y como en muchos centros académicos el trabajo interdisciplinario no solo nunca formó parte de la definición del campo y de los problemas, sino que choca contra otras formas de definir campos y problemas, es inevitable encontrar una fuerte resistencia.
Quizás parezca míope presentarlo en estos términos, pero en el fondo el éxito de un programa u el otro es una cuestión política.
Un abrazo.
Estoy de acuerdo en que Bateson y Bertalanffy plantearon las cosas del lado de los problemas más que de las soluciones - y ese es el punto: la definición de un campo de investigación tiene que ver con los problemas que uno se plantee. La pauta que conecta es un problema y un proyecto, antes que una meta. Y como en muchos centros académicos el trabajo interdisciplinario no solo nunca formó parte de la definición del campo y de los problemas, sino que choca contra otras formas de definir campos y problemas, es inevitable encontrar una fuerte resistencia.
Quizás parezca míope presentarlo en estos términos, pero en el fondo el éxito de un programa u el otro es una cuestión política.
Un abrazo.
a) nunca dije que la solución de Fermat fuera fácil...
b) el premio estaba hacía casi 100 años asi que, eso de que ayudó bastante es discutible.
c) Wiles resolvió el teorema de Fermat. Al menos, así lo decidio la comunidad matemática. A mi no me consta, porque las técnicas que utilizó Wiles me exceden... apenas soy un simple cientista social. Pero lo resolvió. Ahora, lo que supuestamente hizo fue tomar problemas que ya existían y basarse en ellos. Claro que no lo hizo solo. Nunca nadie hace nada "solo". Y sí, mas allá de la demostración de Fermat, el tipo unificó campos de investigación que estaban separados.
d) El planteo del problema es el primer paso para la investigación. El primero y quizás el más importante, porque de esto depende el éxito o no de una investigación: de un problema bien planteado. Ahora, la investigación no se queda ahí. La investigación avanza en la resolución del problema, o no se llama investigación, sino a lo sumo especulación. Puede resolverlo o no. Eso es otra cuestión. Pero tiene que tratar. Esto no quita, obvio, que grandes científicos se destaquen no tanto por resolver los problemas, sino por ponerlos de manifiesto. Pero creo que es otra discusión.
Además el planteo del problema no se deja "librado a la intuición". Eso es volver al planteo del "contexto de descubrimiento" neopositivista (que han tenido muchos aciertos, pero abandonar ese momento ha sido un error). El planteo de un buen problema de investigación es un oficio. Es "aprendible" como cualquier oficio. Y juega tanto la intuición, como la correcta internalización de las normas, formas y demás artificios del trabajo científico.
Tengo que salir... la sigo en un rato.
Abrazos a ambos!!!
Abrazo